Robust Design Optimization - Robust Reliability

Im Gegensatz zu den beiden anderen Methoden (TM, AD) gibt es bei der Robust Design Optimization keine konkrete Vorgehensweise, wie das Problem gelöst werden soll. Es handelt sich bei dieser Methodik lediglich um allgemeine Techniken, die auf die Verbesserungen der Robustheit abzielen. Mögliche Techniken sind zum Beispiel die Anpassung der Zielfunktion oder die Anpassung der Randbedingungen. Beide Techniken werden im Folgenden kurz erläutert.

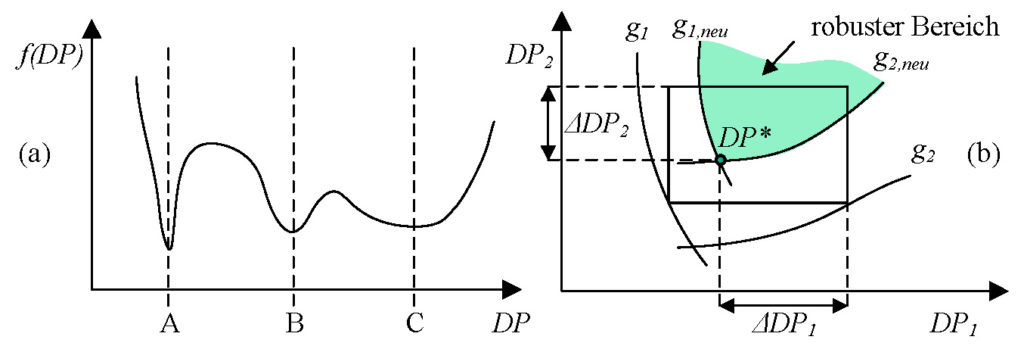
Bild 1.2.3 Robust Design Optimization

Anpassung der Zielfunktion
Bei der Anpassung der Zielfunktion geht es darum, den Parameter so zu wählen bzw. anzupassen, dass eine Schwankung einen möglichst geringe Auswirkung hat. Graphisch betrachtet bedeutet es, das Eingangssignal in einen Bereich zu legen, in dem die Steigung geringer ist. Im Bild 1.2.3 (a) ist im Fall eins der Design Parameter A in einem Bereich, in dem die Empfindlichkeit (Steigung) des Systems deutlich höher ist. Im zweiten Fall befindet sich Design Parameter C in einem Bereich, an dem die Steigung deutlich geringer ist.

Anpassung der Randbedingungen
Die Randbedingungen für die jeweiligen Parameter werden so verkleinert, dass sich die Werte der Parameter immer in dem vorgegeben Toleranzen befinden und damit zulässig sind. Die Grenzen teilen das Diagramm in einen robusten und einen nicht robusten Bereich auf. Bild 1.2.3 (b) zeigt den Einfluss zwei Design Parameter DP₁ und DP₂ auf ihre Zielgröße. Im ursprünglichen Zustand g₁ und g₂ wirkt sich eine Veränderung der Eingangsgrößen DP₁ und DP₂ durch Störeinflüsse erheblich auf den Wert der Zielbereich aus. Somit handelt es sich um ein nicht robuste Parametereinstellung. Im weiteren Zustand wirkt sich eine Veränderung der Eingangsgrößen in den Zustände g_1,neu und g_2,neu nur geringfügig auf den Wert des Zielbereichs aus. Damit ist dieser Zustand unempfindlich gegenüber Störgrößen und laut Definition robust. Die Streuung des Zielbereichs ist somit maßgeblich ausschlaggebend für die Robustheit. Im Idealfall ist der Peak der Zielgröße relativ spitz und die Steigung der Einflusskurve möglichst gering.