Kosten und Zeit spielen in der Entwicklung von Produkten eine große Rolle. Es werden immer wieder neue Herangehensweisen gesucht, mit dem Ziel, die Kosten in der Versuchsplanung sowie -durchführung und die dabei benötigte Zeit zu verringern. Um dies zu ermöglichen, müssen schon im Vorfeld bei der Entwurfsfindung und -auswertung Schwachstellen oder Fehler erkannt und Gegenmaßnahmen eingeleitet werden. Der aktuelle Forschungsstand am Institut für Maschinenelemente der Universität Stuttgart ist in Bild 5.1 aufgezeigt.
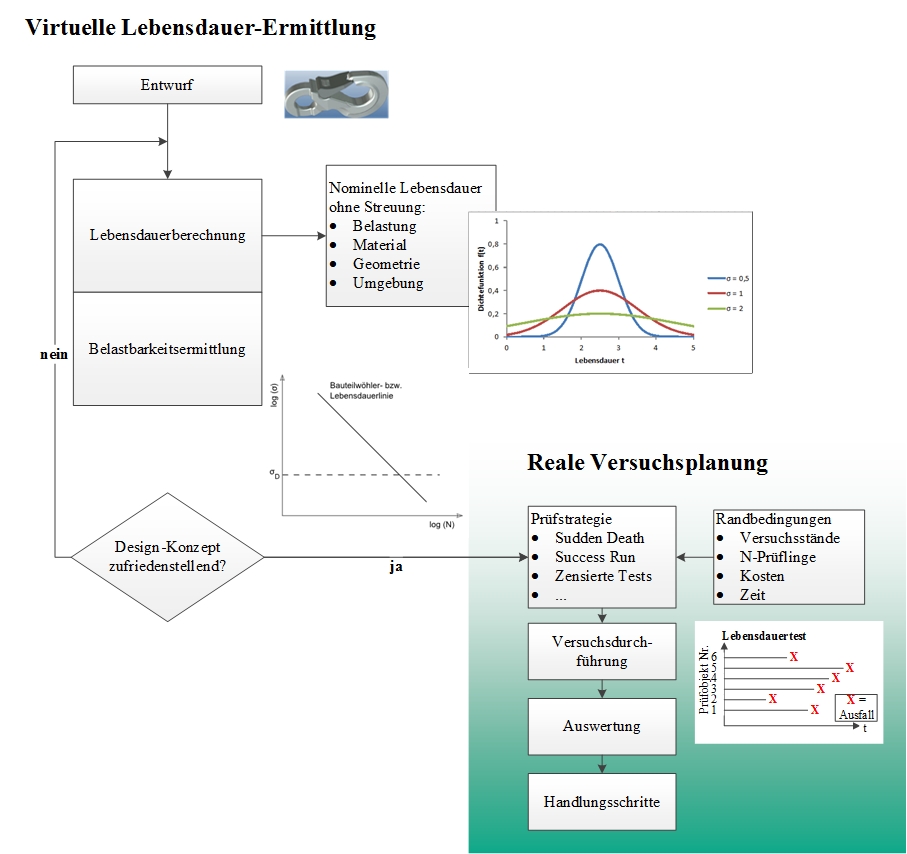
Bild 5.1 Aktueller Forschungsstand
Um die Belastbarkeit des Produktes zu untersuchen, wird anhand eines Entwurfs die Lebensdauer nominell ohne Streuung bestimmt. Mit den ermittelten Kennwerten – der virtuellen Lebensdauerverteilung sowie der Lage der Vertrauensbereiche – wird die Prüfstrategie festgelegt und die realen Versuche werden durchgeführt. Die einzelnen Schritte werden in den folgenden Kapiteln näher erläutert.
Das Ziel, das mit der Virtuellen Lebensdauer-Erprobung 1.0 (VLE 1.0) verfolgt wird, ist die Generierung eines Lebensdauermodells, das die Streuungen der Parameter Belastung, Material, Geometrie und Umgebung berücksichtigt. Daraus ergibt sich eine Lebensdauer, die eine exaktere Prognose über das Bauteil treffen kann als eine Lebensdauer ohne Unsicherheiten.
VLE 2.0 geht einen Schritt weiter. Hier werden zusätzlich die Streuungen der Vertrauensbereiche ermittelt und ausgewertet. Dies wirkt sich vorteilhaft auf die reale Versuchsplanung aus, da diese sich genauer vorbereiten und damit optimiert durchführen lässt. Ziel ist – beispielsweise im Lastenheft gefordert – eine Aussagesicherheit von 90% für die -Lebensdauer im 90%-Vertrauensbereich zu erhalten. Konkret bedeutet dies, dass sich 90 von 100 Fällen in diesem Bereich befinden.
Die Methode VLE gibt explizit aufeinanderfolgende Schritte mit Handlungsempfehlungen vor und gliedert sich in die SMAR²T-Methode ein. Aus dem Zusammenspiel von SMAR²T und VLE soll ein robustes und zuverlässiges Produkt mit einer optimierten realen Versuchsplanung entstehen.
In den folgenden Kapiteln werden die VLE 1.0 mit den drei Phasen – virtuelle Lebensdauer-Ermittlung, virtuelle Lebensdauerversuche und reale Versuchsplanung – näher erläutert.
Virtuelle Lebensdauer-Erprobung 1.0
Um eine effektivere reale Versuchsplanung verwirklichen zu können, werden zuvor virtuelle Lebensdauerversuche eingesetzt. Diese sollen die Auswirkungen der Streuungen auf die Lebensdauer abschätzen und als Ergebnis eine verbesserte Lebensdauerverteilung liefern.
VLE 1.0 unterteilt sich in drei Phasen: die virtuelle Lebensdauer-Ermittlung, die virtuellen Lebensdauerversuche und die reale Versuchsplanung. In Phase I wird die Lebensdauerlinie nominal auf der Einstellstufe (Median) bestimmt. Diese Kurve bildet die Basis für die simulative Berechnung der Streuungen in der Phase II. Die Erkenntnisse aus Phase I und Phase II werden in der realen Versuchsplanung (Phase III) umgesetzt.
In Bild 5.2 sind die einzelnen Phasen und deren Abfolge dargestellt. Phase II gliedert sich dabei in den aktuellen Forschungsstand zwischen Phase I und Phase III ein.
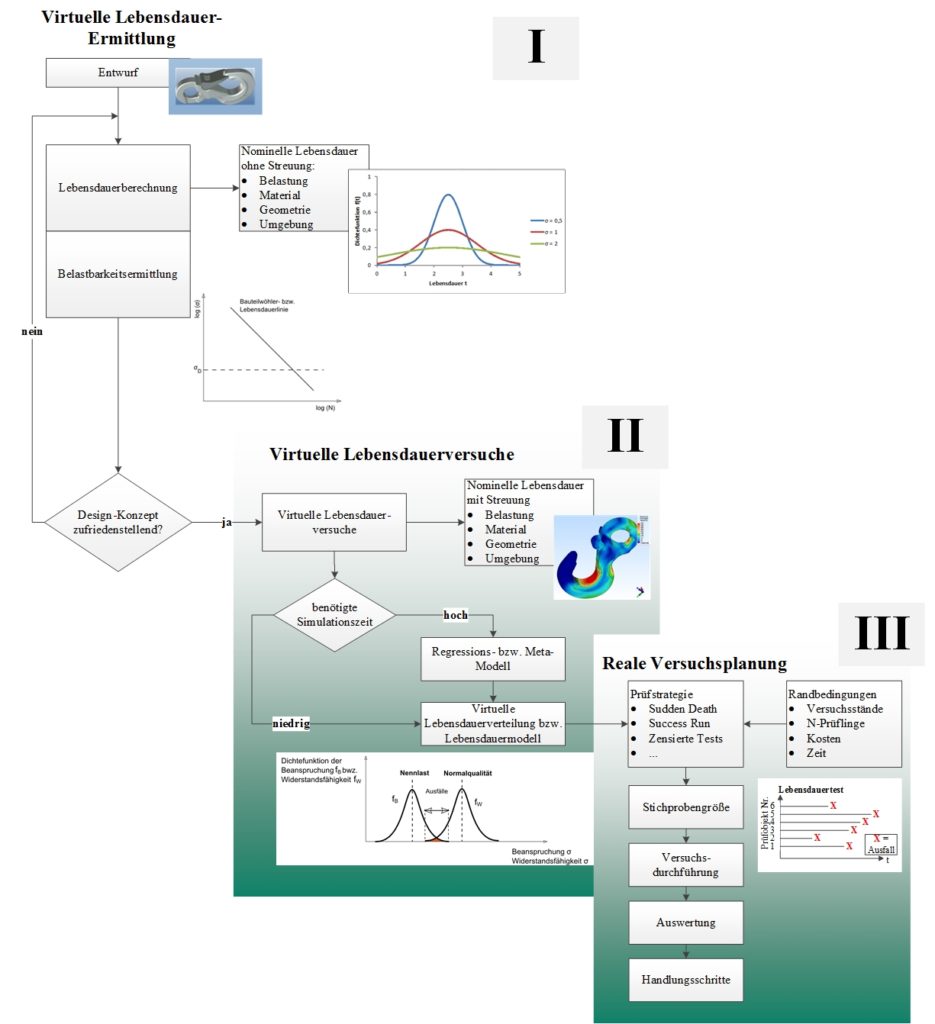
Bild 5.2: Virtuelle Lebensdauer-Erprobung 1.0
Virtuelle Lebensdauer-Ermittlung
Die erste Phase der VLE ermittelt die Basisdaten (Wöhlerkurve, Lebensdauerlinie), die die Grundlage für die Zuverlässigkeitsprognose bilden. Erst wenn ein Design-Konzept gefunden ist, kann in die nächste Phase übergegangen werden. Bild 5.2 beschreibt die auszuführenden Schritte in Phase I.
Ein erster Entwurf (z.B. modelliert in CAD) hält die Kundenanforderungen fest. Im Simulationsprogramm (z.B. ANSYS) werden die spezifischen Werkstoffkennwerte – wie beispielsweise E-Modul, G-Modul, Oberflächenrauheit – für das Simulationsmodell hinterlegt. Danach erfolgt die nominelle Lebensdauerberechnung ohne Streuung anhand einer Definition der Belastung, des Materials, der Geometrie und der Umgebung auf den Median ( -Einstellstufe).
Im nächsten Schritt wird die Belastbarkeit des Bauteils berechnet. Hierfür werden bereits gemessene Daten (z.B. beim Fahrzeug die Streckendaten) und ein Algorithmus benötigt. Am Simulationsmodell werden unterschiedliche Lastwechsel angelegt. Dies kann beispielsweise durch die Verknüpfung der FKM-Richtlinie mit einer FEM-Analyse in ANSYS erfolgen. Aus den einzelnen Schwingspielen wird ein Lastkollektiv mit Hilfe von Klassierungsverfahren (z.B. Klassengrenzüberschreitungsverfahren oder Rainflowzählung) erstellt [1]. Bild 5.3 zeigt die ermittelte Beanspruchungs-Zeit-Funktion und das daraus ermittelte Lastkollektiv.
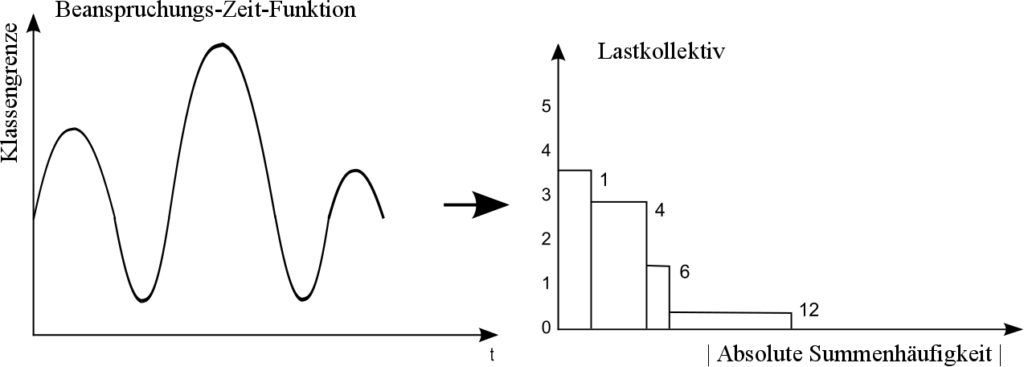
Bild 5.3: Ermittlung eines Lastkollektivs
Für die Ermittlung der ertragbaren Belastung wird das Bauteil bis zum Ausfall bzw. bis zur Werkstoffermüdung belastet. Daraus lässt sich die Wöhlerlinie ermitteln (vgl. Bild 5.4). Die Lastamplitude ist hier logarithmisch über den Lastwechseln aufgetragen. Für jede Ausfallart besitzt eine bestimmte Wöhlerlinie [1].
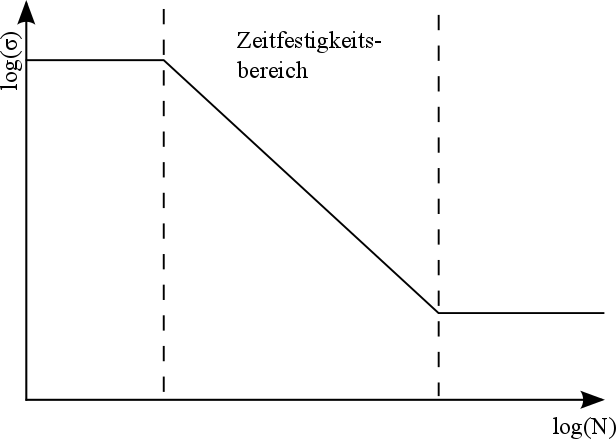
Bild 5.4: Wöhlerlinie
Es gibt drei Konzepte, um aus einem Lastkollektiv und der Wöhlerlinie die Lebensdauer zu berechnen: das Nennspannungskonzept, das örtliche Konzept (Kerbgrundkonzept) und das Bruchmechanikkonzept. Das letztere ist hier nicht relevant, da es von einem bestehenden Riss im Bauteil ausgeht. Beim Nennspannungskonzept wird die Beanspruchung mit der Bauteilwöhlerlinie verglichen. Im Gegensatz dazu wird beim örtlichen Konzept die Werkstoffwöhlerlinie hinzugezogen und der Beanspruchung gegenübergestellt [1].
Um eine Aussage über die Lebensdauer des Bauteils treffen zu können, muss eine Schadensakkumulationshypothese (z.B. Miner original, Miner-Haibach, Corten-Dolan) angewendet werden. Diese kann auf Basis der Daten des zuvor aufgestellten Lastkollektivs und der Wöhlerlinie die Lebensdauer berechnen und eine erste Prognose erstellen. Mit nachfolgender Formel 5.1 kann die Lebensdauer ermittelt werden. Dabei ist die Schwingspielzahl bei der Dauerfestigkeit und die Steigung der Wöhlerlinie [1].
![Rendered by QuickLaTeX.com \[ L=N_D \cdot \frac{\sum_{i=1}^{j+m} n_i}{\sum_{i=1}^{j} n_i \cdot \left( \frac{\sigma_D}{\sigma_i} \right)^k} \qquad (5.1) \]](https://www.robust-reliability.com/wp-content/ql-cache/quicklatex.com-07954ab27778a7cf64ffed343c572ab2_l3.png)
In Bild 5.5 ist die aus der Schadensakkumulationshypothese entstandene Bauteilwöhler- bzw. Lebensdauerlinie dargestellt.
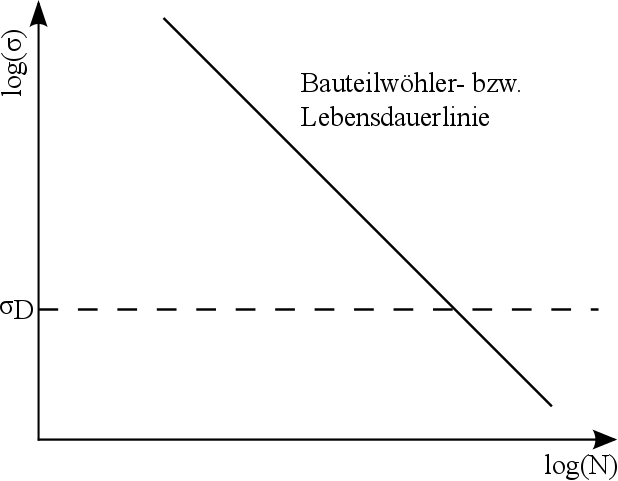
Bild 5.5: Bauteilwöhlerlinie
Ist das entstehende Design-Konzept nicht zufriedenstellend, muss es solange optimiert werden, bis die gewünschten Parameter erreicht sind. Danach können die virtuellen Lebensdauerversuche geplant werden.
Virtuelle Lebensdauerversuche
Bei den virtuellen Lebensdauerversuchen wird die Streuung der einzelnen Parameter Belastung, Material, Geometrie und Umgebung in der Berechnung der Lebensdauer berücksichtigt, um somit eine exaktere Lebensdauerverteilung zu erhalten.
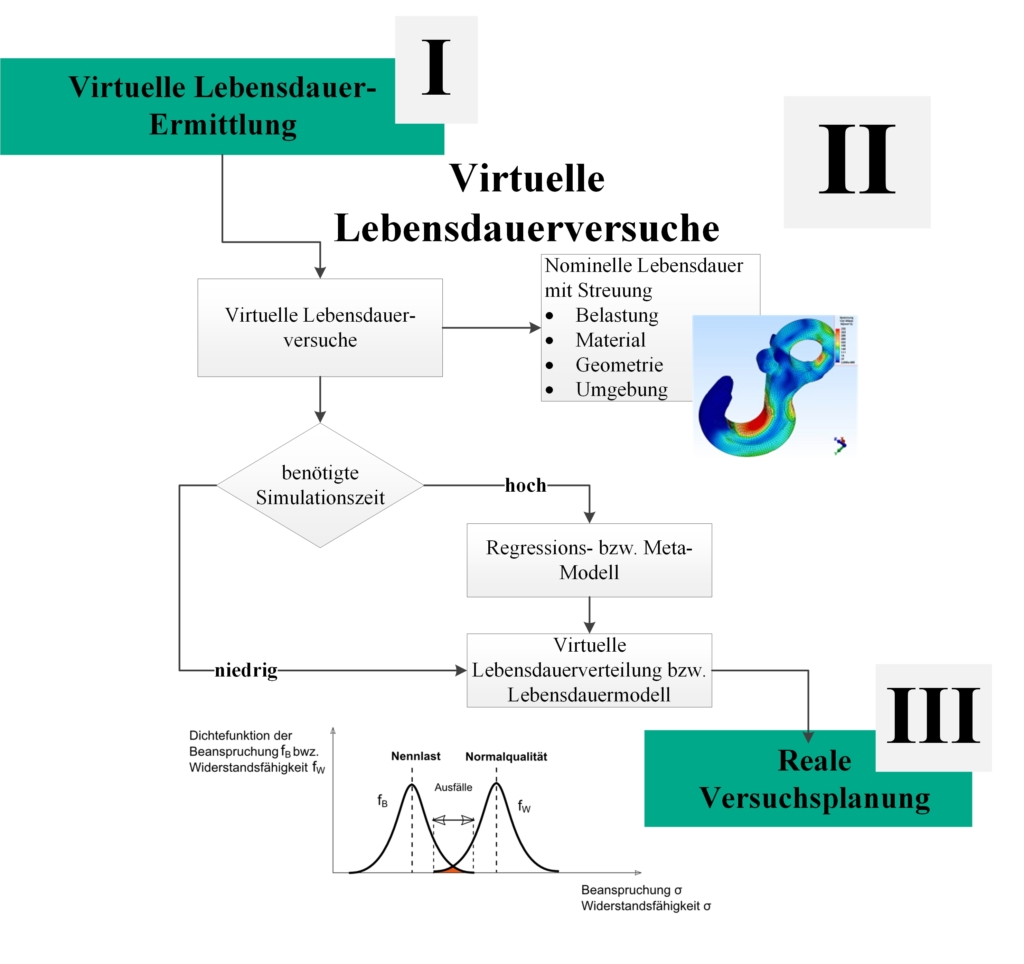
Bild 5.6: Phase II: Virtuelle Lebensdauerversuche
Zuerst muss abgeschätzt werden, wie hoch die benötigte Simulationszeit ist. Dabei ist es wichtig, die geforderten Kosten und die geforderte Zeitdauer aus dem Lastenheft zu beachten. Je komplexer das zu berechnende Simulationsmodell ist, desto höher ist die Simulationszeit. Um diese zu verringern, wird ein Regressionsmodell bzw. Meta-Modell über ein Monte-Carlo- oder Latin-Hypercube-Sampling generiert. Hier wird das Latin-Hypercube-Sampling vorgezogen, da dieses den ganzen Design-Raum abdeckt und eine geringe Korrelation zwischen den einzelnen Faktoren (Dimensionen) aufweist. Anhand des erstellten Meta-Modells wird wiederholt das Latin-Hypercube-Sampling angewendet, um für die definierte Eingangsgrößen die streuenden Ausgangsgrößen auszuwerten. Es entsteht eine Häufigkeitsverteilung, die sich wie in Bild 5.7 darstellen lässt.
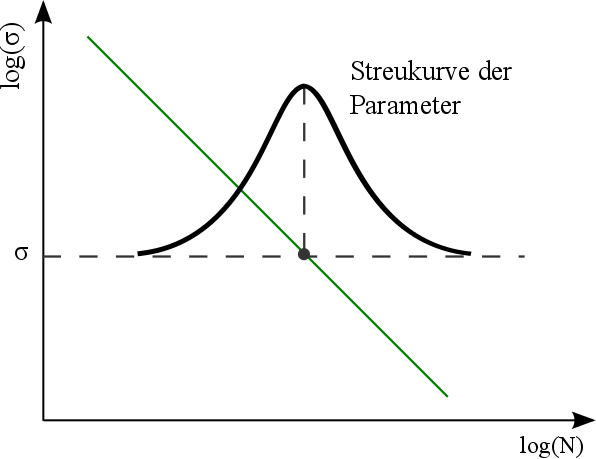
Bild 5.7: Virtuelle Lebensdauerverteilung
Bei geringer Simulationszeit wird direkt im Simulationsmodell die Lebensdauerverteilung über das Latin-Hypercube-Sampling ermittelt. Es entsteht das virtuelle Lebensdauermodell. Durch die Kenntnis des Streuverhaltens kann in Phase III – der realen Versuchsplanung – die Prüfstrategie optimal ausgewählt werden.
Reale Versuchsplanung
Anhand der Zuverlässigkeitsprognose und damit der Kenntnis der virtuellen Lebensdauerverteilung aus dem virtuellen Lebensdauerversuch kann die Wahl der Prüfstrategie optimal getroffen werden. Phase III der VLE zeigt im Rahmen der geforderten Bedingungen aus dem Lastenheft mögliche Handlungsschritte auf (vgl. Bild 5.8).
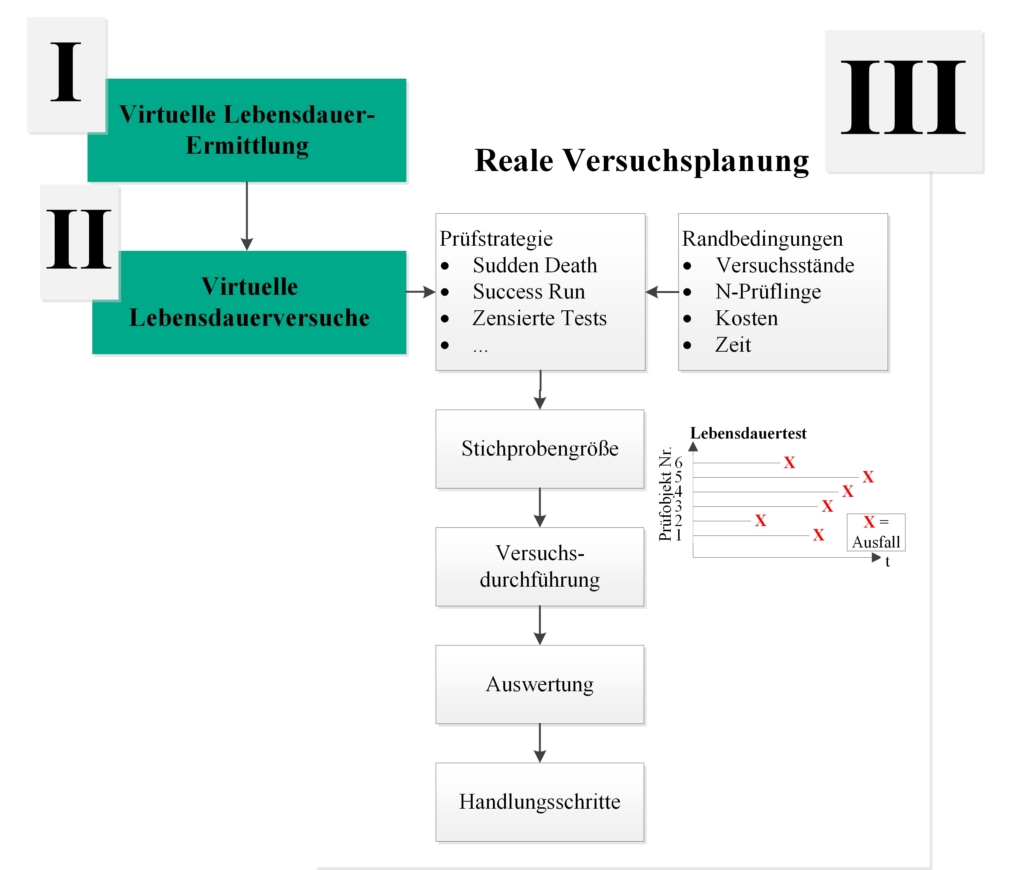
Bild 5.8: Phase III: Reale Versuchsplanung
Die geforderten Bedingungen aus dem Lastenheft müssen eingehalten werden. Die Entscheidung über ihre Umsetzung wird nach individuellen Gegebenheiten im Unternehmen vom Entwickler vorgenommen. Die Anzahl der Versuchsstände und der benötigten Prüflinge sowie die Kosten- und Zeitspanne spielen hier eine Rolle.
Bei der Wahl der Prüfstrategie wird zwischen drei verschiedenen Testarten unterschieden. Vollständige Tests sind statistisch die bessere Wahl, da die Stichprobe vollständig bis zum Ausfall getestet wird. Hier bei der VLE müssen jedoch Zeit und Kosten möglichst gering gehalten werden. Daher werden die vollständigen Tests nicht verwendet. Optimaler sind in diesem Fall unvollständige bzw. zensierte Tests oder Strategien zur Testzeitverkürzung. Bei den zensierten Tests wird entweder nach vorgegebener Zeit oder nach einer vorgegebenen Anzahl an Ausfällen gestoppt (vgl. Bild 5.9). Der Vorteil dieser Teststrategie liegt im geringeren Prüfaufwand und damit verbunden kann eine schnellere Prognose über die tatsächliche Lebensdauer getroffen werden. Zu den Strategien der Testzeitverkürzung zählen Sudden Death oder Success Run. Bei Sudden Death müssen alle Stichproben nach einer vorgegebenen Zeit ausgefallen sein. Dafür wird die Stichprobe in gleich große Prüflose aufgeteilt (z.B. bei 30 Stichproben gibt es 6 Prüflose mit jeweils 5 Teilen). Innerhalb jedes Prüfloses werden die Proben so lange getestet, bis ein Teil ausgefallen ist. Im Gegensatz dazu müssen bei Success Run alle Stichproben nach dem Test noch funktionsfähig sein [1].
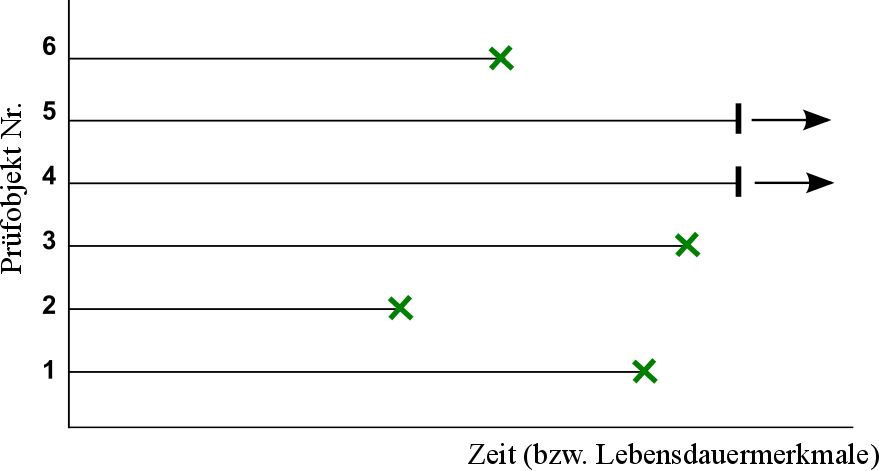
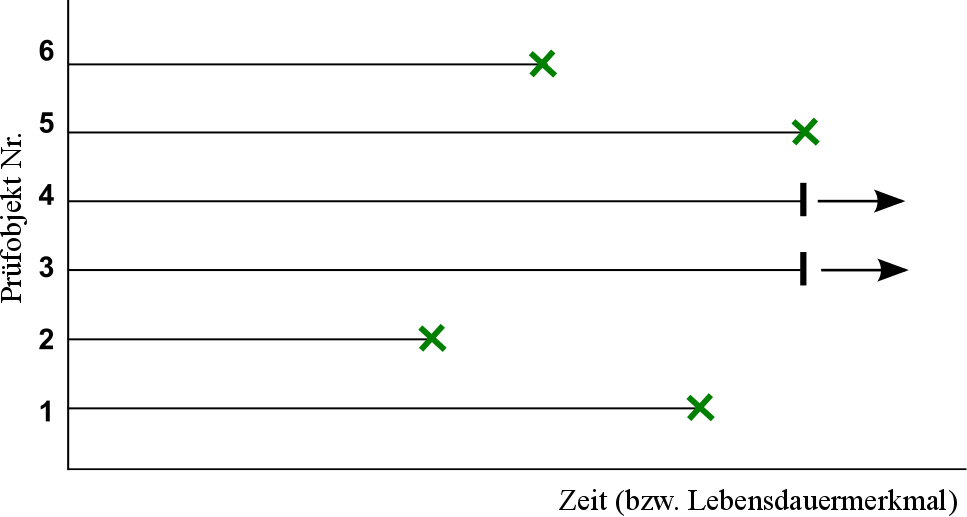
Bild 5.9: Unvollständige bzw. zensierte Tests – links: Zensierung nach Anzahl | rechts: Zensierung nach Zeit
Nach ausgewählter Prüfstrategie kann abgeschätzt werden, welchen Umfang die Stichproben haben sollen. Dies kann zum Beispiel durch Vorkenntnisse von bereits durchgeführten Versuchen oder von Normwerten aus anderen Bereichen erfolgen.
Die reale Versuchsplanung ist damit abgeschlossen und die Versuche können durchgeführt werden. Die sich daraus ergebenden Daten werden ausgewertet. Wenn die gewünschte bzw. geforderte Lebensdauer nicht erreicht ist, müssen Optimierungsschritte unternommen werden. Eine Verbesserung des Entwurfs hinsichtlich einer Neueinstellung der Parameter und damit das Zurückgehen zum Anfang der VLE ist eine Möglichkeit. Die andere kann eine optimierte Lebensdauer durch Veränderung der Stichprobengröße und erneute Versuchsdurchführung liefern.
Ist die geforderte Lebensdauer erreicht, kann das Produkt zur Produktion freigegeben werden.
Virutelle Lebensdauer-Erprobung 2.0
Während der Ausarbeitung der VLE 1.0 hat sich ein weiterer Aspekt ergeben. Zusätzlich zu der virtuellen Lebensdauerverteilung kann auch der Vertrauensbereich virtuell bestimmt werden (vgl. Bild 5.10; Phase IV). Deswegen wird die VLE 1.0 zur VLE 2.0 erweitert.
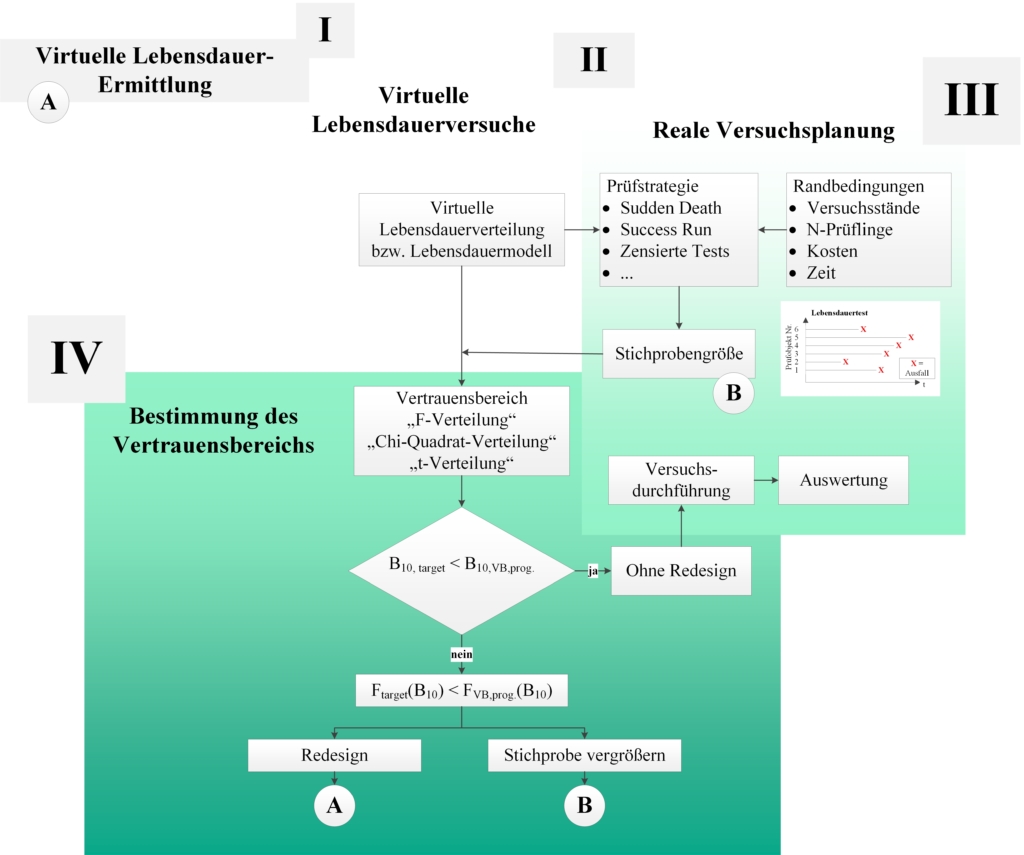
Bild 5.10: Virtuelle Lebensdauer-Erprobung 2.0
Bestimmung des Vertrauensbereichs
Aus der in der realen Versuchsplanung festgelegten Stichprobengröße und aus der virtuellen Lebensdauerverteilung von den virtuellen Lebensdauerversuchen lässt sich der Vertrauensbereich ermitteln.
Mit Hilfe von Verteilungen, wie der F-Verteilung, der Chi-Quadrat Verteilung oder der studentschen t-Verteilung, lässt sich der Vertrauensbereich ermitteln. Tabelle 5.1 zeigt die drei Verteilungsarten auf [2]. Es wird jeweils die obere und untere Vertrauenskurve separat berechnet.
Die studentsche t-Verteilung ermittelt den Vertrauensbereich für den Mittelwert μ der Grundgesamtheit. Der Mittelwert der Stichprobe sowie der Mittelwert der Grundgesamtheit (μ) werden mit sinkender Stichprobenanzahl unsicherer, deshalb wird die studentsche t-Verteilung anstatt der Standard-Normalverteilung angewendet. Im Gegensatz dazu berechnen die F-Verteilung und die Chi-Quadrat-Verteilung den Vertrauensbereich für die Standardabweichung σ der Grundgesamtheit. Die Werte der verteilungsspezifischen Faktoren können aus den Tabellen des Anhangs entnommen werden.
Tabelle 5.1: Ermittlung des Vertrauensbereichs

Versuchsinterpretation
Nun muss das Ergebnis mit den geforderten Werten aus dem Lastenheft verglichen werden. Hier wird die relative Lage des prognostizierten Median zum geforderten Median ermittelt. Es muss gelten:
![]()
bzw.
![]()
Dabei entspricht der Zielwert Ftarget(B10) der geforderten Ausfallwahrscheinlichkeit im Lastenheft und FVB,prog.(B10) der Ausfallwahrscheinlichkeit des prognostizierten 50%-Vertrauensbereichs. Treffen die Gleichungen 5.2 sowie 5.3 auf das Design-Konzept zu, tritt Fall I ein. In der Abbildung 5.11 ist die Ausfallwahrscheinlichkeit F(t) über der Zeit t aufgetragen. Die Farbe blau kennzeichnet den prognostizierten Vertrauensbereich, der zum prognostizierten Median symmetrisch ist. Die Ausfallwahrscheinlichkeit von 10% und die geforderte B10-Lebensdauer schneiden sich im Punkt Ftarget(B10), der den Bezugspunkt im weiteren Vorgehen darstellt.
Fall I bedeutet, dass der Zielwert innerhalb des Vertrauensbereichs liegt. Damit besitzt dieses Design-Konzept eine höhere Ausfallwahrscheinlichkeit. Das Design-Konzept erfüllt nicht die geforderte Lebensdauer und es müssen Gegenmaßnahmen eingeleitet werden. Eine Vergrößerung der Stichprobe führt zu einer Annäherung der Vertrauensbereiche an den prognostizierten Median und damit zu einer erhöhten Aussagesicherheit.
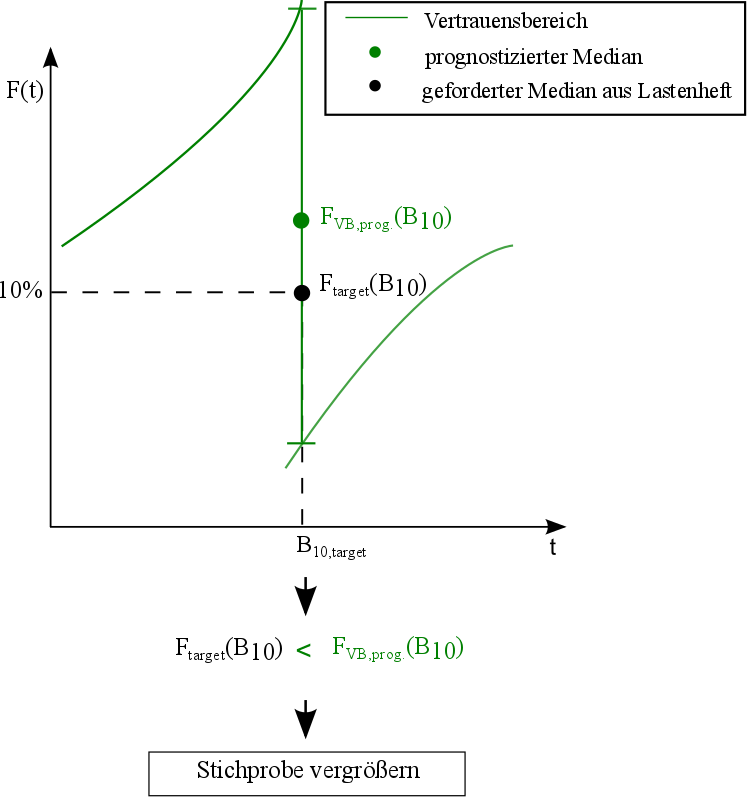
Bild 5.11: Auswertung des Vertrauensbereichs (Fall I)
Durch die Änderung der Stichprobengröße wird eine verbesserte Aussagesicherheit generiert und es können zwei Ergebnisse entstehen:
- der Zielwert liegt außerhalb des Vertrauensbereichs oder
- der Zielwert liegt innerhalb des Vertrauensbereichs.
Das erste Ergebnis ist in Abbildung 5.12 dargestellt. Der Zielwert liegt nicht im Vertrauensbereich und somit ist die Forderung aus dem Lastenheft nicht erfüllt. Daher muss hier ein Redesign erfolgen. Beim Redesign wird entweder ein neues Lösungskonzept erarbeitet oder durch Veränderung der Parameter Material, Belastung, Geometrie und Umgebung in Phase I eine Verbesserung hinsichtlich der virtuellen Lebensdauerverteilung erzielt.
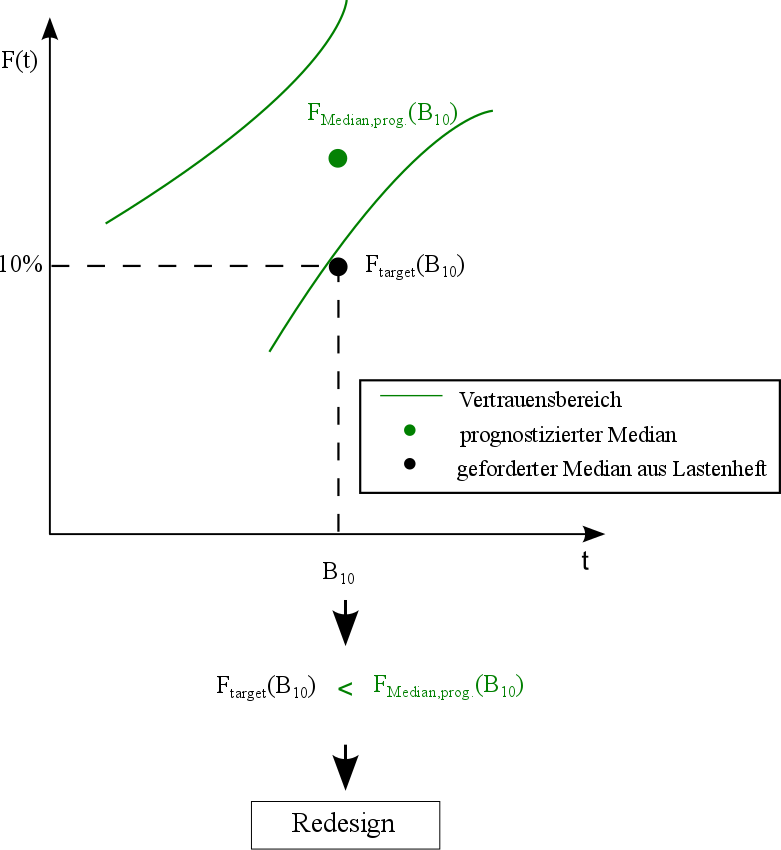
Bild 5.12: Ergebnis nach Verbesserung (1)
Liegt der Zielwert auch nach Vergrößerung der Stichprobe innerhalb des Vertrauensbereichs (vgl. Bilde 5.13), können mit dem ausgearbeiteten Entwurf die realen Versuche durchgeführt werden.
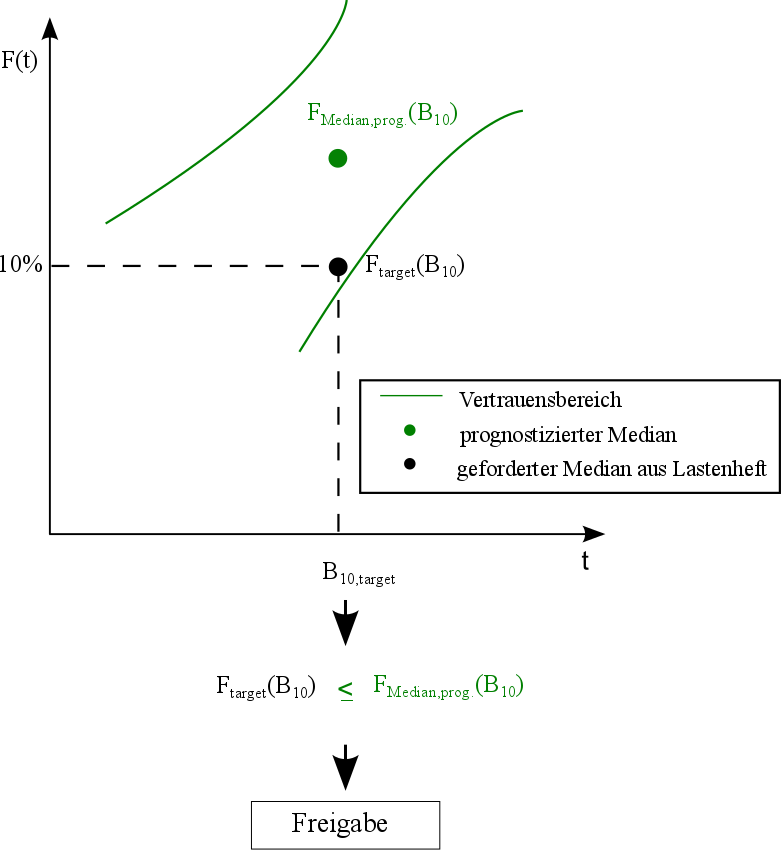
Bild 5.13: Ergebnis nach Verbesserung (2)
Gilt stattdessen
![]()
bzw.
![]()
tritt Fall II (vgl. Bild 5.14) ein. Die B10 -Lebensdauer des prognostizierten Vertrauensbereichs besitzt einen höheren Wert als die geforderte Lebensdauer. Das heißt, das generierte Modell ist exakter als gefordert und besitzt eine geringere Ausfallwahrscheinlichkeit. Das Design-Konzept kann direkt freigegeben werden.
Mit diesem werden die realen Versuche durchgeführt. Danach werden die getesteten Stichproben ausgewertet und das reale Ausfallverhalten des Bauteils kann prognostiziert werden.
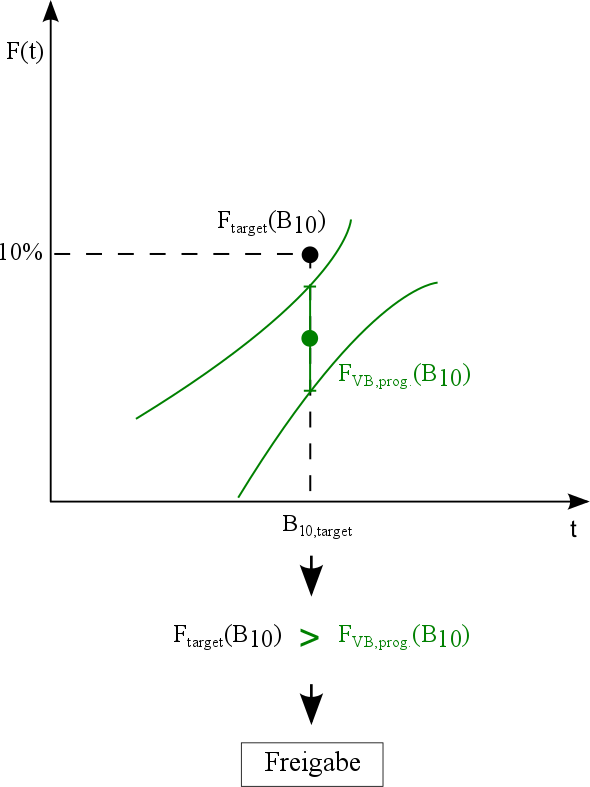
Bild 5.14: Auswertung der Vertrauensbereiche (Fall II)
____________
[1] Bertsche, B., Lechner, G.: Reliability in Automotive and Mechanical Engineering. Berlin, Heidelberg, New York: Springer-Verlag 2007.
[2] ZÖFEL, P.: Statistik verstehen: ein Begleitbuch zur computergestützten Anwendung. Pearson Deutschland GmbH, 2001.


 English
English